Zero Knowledege Proofs, Berkeley Math Circle
These are my notes from a class at the Berkeley Math Circle on October 23rd, 2024. You can find an accompanying handout here.
Today we’ll be talking about spies and secret messages and the question of what it is possible to know.
A quote from the Soviet mathematician VI Arnold:
All mathematics is divided into three parts: cryptography (paid for by CIA, KGB and the like), hydrodynamics (supported by manufacturers of atomic submarines) and celestial mechanics (financed by military and by other institutions dealing with missiles, such as NASA.).
Cryptography has generated number theory, algebraic geometry over finite fields, algebra (the creator of modern algebra, Viete, was the cryptographer of King Henry IV of France), combinatorics and computers.
Hydrodynamics procreated complex analysis, partial differential equations, Lie groups and algebra theory, cohomology theory and scientific computing.
Celestial mechanics is the origin of dynamical systems, linear algebra, topology, variational calculus and symplectic geometry.
Today we have a few more branches as well. What Arnold is saying is that mathematics bears the imprint of the society which produces it. Of course it has its own internal logic to an extent, but we cannot ignore the effect of the society on mathematical development.
This is just to remind us that math is not just some pure thing for fun – it is in a relationship with the rest of the world and needs of society.
Today we will focus on the branch of cryptography, these days paid for not just by the CIA but also the tech companies.
Cryptography’s primary function historically has been in sending secret messages for the purposes of military coordination. Garbling a message so only its intended recipient (hopefully) can read it is called encryption. Encryption in the past was quite simple, and is very easy to break by modern standards.
Modern cryptography really gets started during World War 2. Famously codebreakers including Marian Rejewski, Jerzy Rozycki, Henryk Zygalski, and Alan Turing broke the Nazi’s “enigma code”. The ability of the allies to read Nazis encrypted messages was very important in their winning the war.
The history of cryptography is strongly tied with the history of computing in general. Probably the most famous characters of early computer history, Alan Turing and Claude Shannon, spent a lot of time on studying encryption.
Why the connection? Some reasons:
- Encrypting and decrypting messages is a tedious algorithmic process. If carried out by humans, it would end up leaking the message to those doing the encrypting. Therefore there is a motivation to create a machine to do it instead.
- Similarly for breaking codes: it is clear that code breaking might benefit from a somewhat “brute force” effort of trying many different possible decryptions. Therefore a mechanical method was desired.
- Understanding whether or not a code could be broken requires a theory of what it is possible to compute. This is the question of computability and complexity theory.
Today, encryption is used by all of our devices every time they receive information on the web.
Modern cryptography is about much more than encryption, however. It is about making a system continue to function in the presence of adversarial behavior. What is adversarial behavior? It means someone is trying to cheat or break the system somehow.
Today we’ll be learning about one amazing cryptographic object, which is called a zero-knowledge proof.
Zero-knowledge proofs are a technique for convincing someone of a fact, without them learning anything new other than the fact.
Some examples where this sort of thing is useful:
- I would like to convince a website that I know the right password to get into my account, without having to actually send the password over the internet.
- Let’s say I have a proof of a great theorem, but you don’t believe me. I could convince you that I do actually know the proof without showing it to you, so that you can’t take credit for it.
- I would like to vote in an election, and therefore prove I’m qualified to vote, without my vote being linked to my identity.
Warm-up activities
Where’s waldo demonstration.
Red green activity In groups of 2.
Take turns playing the roles of Prover and Verifier.
You have red and blue pieces of paper. Verifier, you should pretend to be colorblind. The prover’s job is to try to convince you that they can tell the difference between these two pieces of paper even though you are unable to.
What did we learn from these activities?
Proof may involve interaction, it may involve randomness. Is this a proof? How does it differ from the usual notion of proof we see?
It’s possible to convince someone that you can solve a problem even when they can’t solve that problem, and in such a way that they don’t get any information that will help them solve the problem.
ZK for 3-coloring
Now let’s look at a more “practical” problem.
Let’s say I have a bunch of ingredients (ask students for ingredients.)
I am planning up to 3 meals: breakfast, lunch and dinner, and I want to use all the ingredients. The first thing I do is write down which ingredients clash with each other. For example, I don’t want to have peanut butter and ground beef in the same meal. I need to assign ingredients to each of the three meals in
Peanut butter, ground beef, tofu, egg, ketchup, apples.
Let’s say the following pairs should not be in a meal together:
- Peanut butter and ground beef
- Peanut butter and tofu
- Peanut butter and egg
- Peanut butter and ketchup
- Ground beef and apples
- Ground beef and tofu
- Tofu and apples
- Tofu and ketchup
- Egg and apples
- Ketchup and apples
I’m okay with missing a meal as long as I use all the ingredients. Like, if all the ingredients are assigned to breakfast, that’s okay. My main goal is to use all the ingredients.
This problem can be modeled mathematically as follows. The ingredients will be the vertices of a graph, and we will put an edge between them if they shouldn’t be in the same meal. ![[/img/math-circle-talk/foods 3.png]] Now, our goal is to assign the vertices one of 3 colors: red (representing breakfast), green (representing lunch), or blue (representing dinner).
Here’s one way we can do it.

So we’d be eating beef, egg and ketchup for breakfast, tofu for lunch, and apples with peanut butter for dinner.
In general we can look at any graph $G$ and ask if it’s possible to put one of $k$ colors on each vertex so that every edge has different colored endpoints. In other words, every vertex should have a different color from its neighbors.
If it is possible, we say the graph is k-colorable and we call an assignment of colors to vertices a k-coloring.
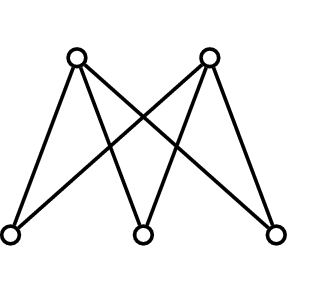

Exercise. Are the above graphs 3-colorable? Why or why not? How would you describe what you are doing to check if the graph is 3-colorable?
For fun (if you know what a tree is): Prove that every tree is 2-colorable. Challenge: Suppose $G$ is a graph with $n$ vertices that requires at least $k$ colors to validly color. Prove that $G$ has at least $\binom{k}{2}$ edges.
Proving
As you maybe found out, actually constructing a coloring can be difficult. And just imagine how hard it would be for a large graph with 1,000,000 vertices.
One thing that’s interesting is while a coloring is hard to come up with, it’s very easy to check. Just go edge by edge and make sure every pair of neighboring vertices have different colors. In other words, once we have done the hard work of finding a 3-coloring, it is not hard to share the fact that a graph is 3-colorables with others. They don’t have to redo all the hard work that we did to see it.
Note that this indeed a special thing that isn’t true of all properties related to graphs. For example, if we wanted to check that a graph was not 3-colorable, in principle we would have to try every possible 3-coloring and check that it fails. In that case, at the end of the check we may be convinced, but there is no short piece of information that we can share with others to spare them doing the same exhaustive check.
However, if you were able to construct a coloring for a large graph, you might want to convince someone that you were able to without showing them the coloring. This might be the case if the coloring was somehow valuable.
For simplicity let’s restrict our attention to 3-colorings. Our goal will be to come up with some method for proving to another person that we have a 3-coloring without them learning anything about that coloring.
Activity: break up into groups of 2. One person tries to convince the other a graph is 3-colorable without showing them the coloring.
Let’s say we are the “prover” who has a 3-coloring, and the person we’re trying to convince is called the “verifier.”
Here is a method:
- Draw the graph on a big sheet of paper. The Verifier leaves the room.
- The Prover shuffles the messages in their coloring at random. That is, red, green, and blue are replaced by a random permutation of those colors. For example, we may replace red with green, green with blue, and blue with red.
- Color the graph according to the shuffled coloring.
- Put cups over the now colored vertices and have the Verifier come back into the room.
- The Verifier selects one of the edges at random and the Prover lifts up the cups on the endpoints of that edge.
- If the two endpoints have different colors, the Verifier takes this as evidence that under the cups is a valid 3-coloring. If the two endpoints have the same color, the Verifier remains unconvinced about the 3-colorability of the graph.
After doing this routine, if the Prover does not really have a 3-coloring, there is some probability that the Verifier will catch them.
Why is there a chance that the Verifier will catch them?
Say there are $m$ edges. What is the probability the Verifier will catch a lying prover?
Now that we know doing this routine once will allow the Verifier to catch the prover with some probability, we have them repeat it many times.
Lying once, you may get away with, but if you try to lie many times, eventually you will get caught at least once.
If we repeat this routine $k$ times, what is the probability that a lying prover will be caught at least once in those $k$ times?
Exercise: Say we are running the protocol with a graph of size 100. How many times do we need to run the protocol for the chance of a cheating prover winning to be less than 1%?
Experiment. Try to figure something out about the coloring given the information from a bunch of random runs of the protocol.
Zero knowledge
We say that this protocol is zero-knowledge. That is, the verifier learns nothing from the interaction. How can we formalize this mathematically? The approach is essentially the following: whatever the verifier is able to compute after the interaction could already have been computed beforehand.
Let’s make this a little more precise. A protocol is zero knowledge is there is a randomized algorithm $S$ which generates output that is indistinguishable from what the verifier sees in an interaction with an honest prover.
More questions
- Are these really proofs? How do they compare to the usual notion of proof that you have seen?
- What kind of problems have short proofs? E.g., we have a short proof for graphs being 3-colorable, but we don’t seem to have one that a graph is not 3-colorable.
- What kind of problems have short proofs that are also zero-knowledge?
Another problem
Recap modular arithmetic.
Here is a problem that can really be used for cryptography. Given a number $x$ in $[0, n-1]$, we can ask if $x$ is a square mod $n$. I.e., is there a number $y$ such that $x = y^2 \mod n$.
For example, $11$ is a square mod $35$ because $9^2 = 81 = 11 + 70 = 11 + 35\cdot 2 = 11 \mod 35$.
Notice that it’s easy to come up with examples by just taking a number and squaring it. So I can start with 20 for instance and find that $20^2 = 400 = 15 + 35 \cdot 11 = 15 \mod 35$ so I know that 15 is a square.
This is not so easy! For example, see if you can find a number $y$ with $y \cdot y = 30 \mod 35$.
Can you convince me that a number is a square without revealing its square root?
Challenge: try to come up with a way of finding out if a number is a square which is better than brute force
